Overview
Multivariable regression is a statistical method that can be used to estimate health care costs for different groups of patients. In the simplest case, the cost of two groups of patients can be compared by using an indicator variable for group membership as the explanatory variable in a model predicting costs. For example, to compare costs of a treatment group with a control group, an indicator variable can be used to assign subjects in the treatment group a value of one and subjects in the control group a value of zero. In a cost regression model, the coefficient for the indicator variable represents the difference in cost associated with being a member of the experimental group compared to the control group. When group assignment is not random, additional independent variables in a regression model controls for the effect of of age, sex, chronic illness, or other factors on costs.
Health care costs are not typically normally distributed. Some patients may incur a lot of costs for their health care, and some patients incur zero costs for their health care. In the former case, the distribution of costs will be right skewed, and in the latter case, the distribution of costs will be truncated. Due to these properties of the cost variable, it is necessary to employ appropriate methods to model costs. These methods are discussed below and are followed by descriptions of applications to VA cost issues such as determining inpatient cost and estimating the effect of chronic illness on health care cost.
Modeling Health Care Costs
The most common multivariable regression method is Ordinarly Least Squares (OLS). This method assumes that the dependent variable is normally distributed and that the errors in the regression are independent and not explained by any of the other independent variables. Since health care costs are highly skewed and not normally distributed, the error terms in cost regressions often violate the assumptions of OLS.
This problem can be overcome by transforming costs, the dependent variable, making it more normally distributed. One common method is to take the natural log of the cost variable. This approach has limitations, but almost always results in less bias than an OLS regression of raw costs. Among the limitations is the impossibility of including observations in which no cost was incurred, as it is not possible to take the log of zero. Substituting a small positive number (e.g., one dollar) for zero costs can result in biased parameters and is not recommended. Simulating costs from a function that uses a transformed dependent variable (such as the log of costs) requires correction for retransformation bias.
Generalized Linear Models (GLM) allow more flexible modeling of costs that are superior to OLS regression of log cost (McCullagh and Nelder, 1989). GLM models allow inclusion of observations with zero cost. Moreover, GLM models correct for heteroscedastic errors and do not need to be adjusted for retransformation bias. GLM consist of three components: the conditional distribution of the response variable, a linear predictor, and the link function. There are specific tests to choose the best link function and most appropriate distribution. A common form of GLM regression uses a log link function and a gamma distribution, and for this reason, is often referred to a gamma regression. Special care must be exercised in running gamma regressions in the SAS statistical program, as the default is to exclude observations that have zero cost as the dependent variable.
Alternatively, a two-part model can be used to handle cost data where there are a large number of observations with zero healthcare expenditures (Deb and Norton, 2017). In a two-part model, the first part of the model estimates whether the subject had any non-zero healthcare expenditure. This can be achieved using either a logit or probit model. The second part of the model is conditional on the first part being positive and can be a GLM, which can give the researcher flexibility to model cost data. Standard errors and 95% Confidence Intervals (CI) can be estimated using "recycled predictions" a method that bootstraps the data as described by Kleinman and Norton (2009). An early application of the two-part model method was conducted by Manning and colleagues (1987) to address the high proportion of study subjects that did not incur expenditures. The Stata package "twopm" allows users to define the first and second part of the models easily (Belotti, et al, 2015)).
For more information on widely used models and how to choose among them, the analyst will want to consult the papers by Manning and Mullahy cited below. Archived presentation on cost regressions are given in the HERC econometrics seminar series and are available on the archived seminars page.
Retransformation Bias
Economists frequently wish to estimate regression models using healthcare cost as the dependent variable. Health data are often strongly skewed to the right, however, making ordinary least squares unattractive. For example, the length of inpatient stays and the cost of inpatient care are often highly skewed (and kurtotic). A common approach is to use the natural log of cost in place of raw cost. The logarithmic transformation often removes enough skewness to allow least squares models to produce unbiased results. The resulting coefficients from such a regression are not directly interpretable in raw dollars. The fitted value of a log-cost regression cannot be exponentiated to estimate cost, as there is a retransformation bias (Manning 1998). Retransformation bias does not occur when simulating costs from parameters estimated from GLM regressions; this is one of several advantages to the GLM approach.
The case of homoskedastic errors: the smearing estimator
If the errors from the regression are homoskedastic, one can determine an appropriate retransformation through the smearing estimator (Duan 1983). Consider a regression model of the form:
![]()
A simulation of the retransformed fitted value (cost) when X=X0 is not simply:
![]()
Although the expected value of the residual is zero, it is subject to a non-linear retransformation. The expected value of cost when X=X0 is thus:
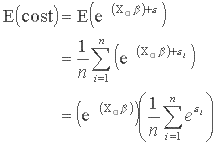
The smearing estimator for models with log-transformed dependent variables is the right hand factor. It is the mean of the anti-log of the residuals:
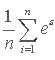
Most regression packages allow the analyst to save the residual. To find the smearing estimator, we find the anti-log of the residuals, and then find its mean. This often yields a value between 1 and 2. The smearing estimator is then multiplied by the fitted value to correct it for retransformation bias. The method in Duan (1983) also applies to other non-linear models, such as a square-root transformation of the dependent variable.
The case of heteroscedastic errors
Quite often the error for a particular observation in the cost regression will depend on the level of one or more regressors. This situation, known as heteroscedasticity, precludes the use of Duan's smearing estimator unless the heteroscedasticity can be modeled accurately. For example, if heteroscedasticity occurred only based on sex, then one could estimate separate smearing estimators for men and for women. The sources of heteroscedasticity may be more complicated in other situations, and in some cases it may be impossible to control for it sufficiently.
There are several alternative approaches to this problem. A technical explanation is beyond the scope of this page; interested readers are encouraged to read the journal articles in the References section below. Mullahy (1998) lays out the econometric problem in detail and derives the bias of the smearing estimator when heteroscedasticity is present. Manning and Mullahy (2001) and Basu et al. (2004) describe several alternatives: ordinary least squares on the natural log of y; GLM variants (such as gamma regression with log link and Weibull regression with log link); and the Cox proportional hazards model. They conclude that no single model is best under all circumstances.
Applications of Cost Regression Methods to VA Data
HERC used cost regressions to estimate the cost of VA hospital stays and to determine the incremental effect of specific chronic diseases on VA health care costs.
Estimating VA Inpatient Costs
HERC Average Cost data uses cost regressions to estimate the cost of VA hospital stays. A cost regression is estimated using non-VA data for Medicare stays of Veterans. Medicare data reported the charges for hospital stays that can be adjusted by a hospital cost-to-charge ratio to obtain an estimated cost. Cost-adjusted charges are the dependent variable and characteristics of the patient, the hospital, and the hospital stay, are the independent variables. The resulting coefficients are used to create predicted costs (fitted values of the dependent variable) for VA hospital stays with particular attributes (levels of the independent variables).
This method is more precise than assuming that every day of hospital stay has the same cost, or that cost is proportionate to Diagnosis Related Group (DRG) weight. It takes advantage of additional information available to explain the costs variations, such as days of stay that are longer than the average for that DRG.
See the page describing the HERC inpatient average cost estimates for more information on this regression analysis.
One limitation of the HERC cost regressions is the lack of information on the cost of physician services. HERC use the cost-adjusted charge from the hospital as the dependent variable, excluding the cost of physicians services. Physicians bill separately from the hospital, and it is difficult to determine which part of the physician reimbursements are attributable to services provided during a hospital stay. VA costs include all physician services, so the predicted cost-adjusted charges based on a non-VA hospital regression understates the true cost of care. HERC adjusts its estimates so that they sum to the total of VA inpatient costs. This assumes that the cost of physician services is proportional to the cost of the hospital component. There are few alternatives to making this assumption. Analysts who need a more specific cost of physician services provided to hospitalized patients would need to merge physician billing data with hospital billing data. A study from 2015 estimated the average professional fee ratio associated with each DRG (Peterson et al., 2015), so facility charges can be adjusted to incorporate professional charges using these ratios.
Studies that rely on this costing method are listed in the bibliography of Technical Report 32: Costing Methods Used in VA Research, 1980-2012.
Regression Studies of the Cost of Chronic Diseases
Researchers at HERC have use cost regression to estimate the incremental effect of common chronic conditions on VA cost. These studies used diagnosis codes from VA encounter records to classify different conditions and obtained estimates of the costs of VA health care from HERC Average Cost estimates. The most recent study estimated the costs and prevalence of 16 conditions in 2000 and 2008 based on two instances of a specific diagnosis in encounter records. An earlier study, based on 1999 data, estimated the costs and prevalence of 40 different conditions and used a less restrictive definition of only a single diagnosis. Both studies used the same multivariate methods to estimate the marginal costs associated with each chronic condition after adjusting for all other conditions and demographic characteristics such as age and sex. For general estimates of the total VA patient population, researchers can contact HERC.
References
Barnett PG. Determination of VA health care costs. Medical Care Research and Review. 2003;60(3 Suppl):124S-141S.
Basu A, Manning WG, Mullahy J. Comparing alternative models: log vs Cox proportional hazard? Health Economics. 2004;13(8):749-765
Belotti F, Deb F, Wanning WG, Norton EC. twopm: Two-part models. The Stata Journal. 2015;15(1):3-20.
Deb P, Norton EC. Modeling Health Care Expenditures and Use. Annu Rev Public Health. 2018 Apr 1;39:489-505.
Duan N. Smearing estimate: a nonparametric retransformation method. Journal of the American Statistical Association. 1983;78:605-610.
Kleinman LC, Norton EC. What's the Risk? A simple approach for estimating adjusted risk measures from nonlinear models including logistic regression. Health Serv Res. 2009 Feb;44(1):288-302.
Manning WG. The logged dependent variable, heteroscedasticity, and the retransformation problem. J Health Econ. 1998;7:283-95.
Manning WG, Mullahy J. Estimating log models: to transform or not to transform? J Health Econ. 2001;20:461-94.
Manning WG, Basu A, Mullahy J. Generalized modeling approaches to risk adjustment of skewed outcomes data, J Health Econ, 2005;24:465-88.
Manning WG. Dealing with skewed data on costs and expenditures, in: Jones, A. (Ed.) The Elgar Companion to Health Economics, 2006; pp. 439-446 (Cheltenham, UK, Edward Elgar).
Manning WG, Newhouse JP, Duan N, Keeler EB, Leibowitz A, Marquis MS. Health insurance and the demand for medical care: evidence from a randomized experiment. Am Econ Rev. 1987 Jun;77(3):251-77.
Manning WG, Mullahy J. Estimating log models: to transform or not to transform. Journal of Health Economics 2001;20:461-494.
McCullagh P and Nelder JA. Generalized Linear Models. Second Edition. Chapman and Hall/CRC (August 1, 1989).
Miller ME, Welch WP. Analysis of Hospital Medical Staff Volume Performance Standards: Technical Report. Washington, DC: Urban Institute, 1993.
Mitchell JB, McCall NT, Burge RT, Boyce S, Dittus R. Heck D, Parchman M, Iezzoni L. Per Case Prospective Payment for Episodes of Hospital Care. NTIS report PB95226023. Waltham, MA: Health Economics Research, 1995.
Mullahy J. Much ado about two: reconsidering retransformation and the two-part model in health econometrics. Journal of Health Economics 1998;17:247-281.
Last updated: April 24, 2023














